After our introductory post on Network Strategy, many people reached out to us asking about the distance formula that we used to calculate the distance between two points.
After our introductory post on Network Strategy, many people reached out to us asking about the distance formula that we used to calculate the distance between two points.
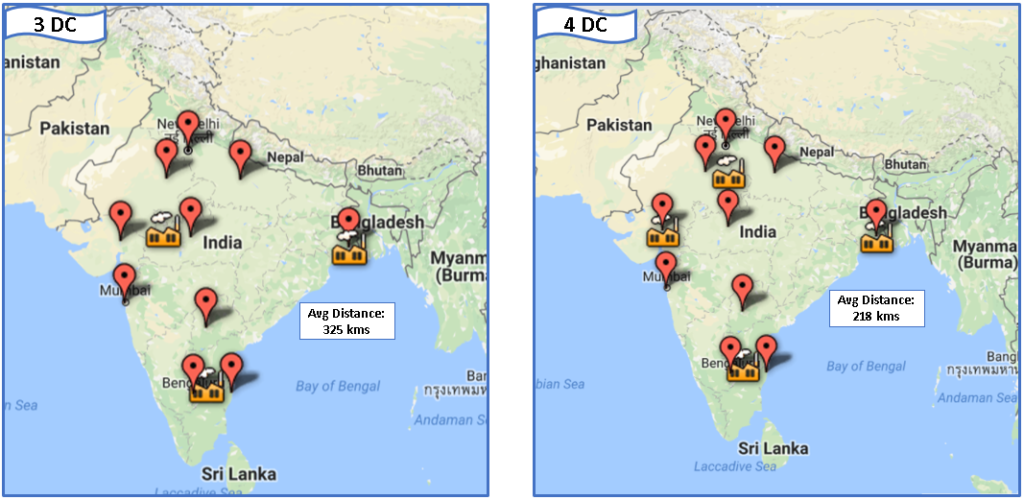
Distances between plants, DCs and customers are the key things that impact supply chain design and customer service levels. So, we have decided to cover this topic in a short post to arm you with all the ultra-useful tools you’d need to calculate the distance between two points. If you are just looking to calculate distances based on Latitude and Longitude of the two locations, you can directly skip to section 3.
If you are just looking for an excel file with Spherical distance formula with Lat-Long, download it here.
1. Cartesian Distance
2.Taxicab Distance/ Manhattan Distance
3.Spherical Distance (Law of cosines)
Cartesian Distance
Dusting-off our high school mathematics, there is a very direct formula to calculate distance between two points if you know their coordinates. Let us refresh our memories.
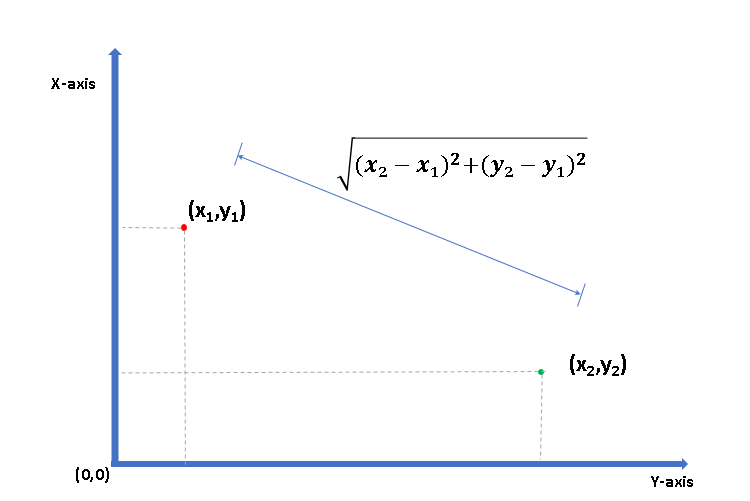
So if the two points are (1,5) and (6,2) respectively then the distance between them is 5 units.
Taxicab Distance/ Manhattan Distance
When we are dealing with planned urban areas, especially a grid of roads covering the city like Manhattan (hence the name Manhattan distance), we’ll have to travel along the grid to reach from one point to another.
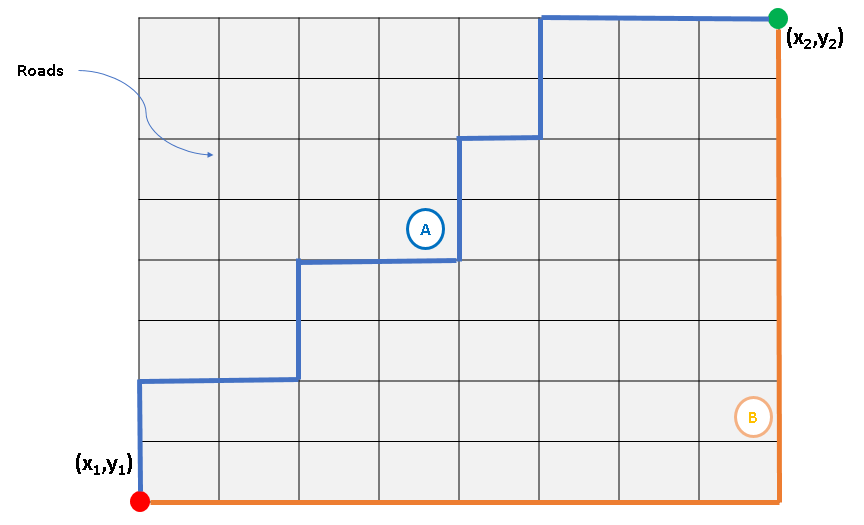
In such cases, the distance travelled is simply |x2-x1| + |y2-y1| and remains the same for all possible routes as long as we are moving towards the destination point. In the above example where the grid is 8 x 8 units, we’ll have to travel 16 units.
Taxicab distance or Manhattan distance is quite useful while calculating last mile delivery distances in planned urban areas.
Spherical Distance (Or "As the Crow Flies" distance)
Question: What would you do if I asked to travel from point A to point B on the surface of the Earth in the shortest distance?
Answer: Dig a tunnel.
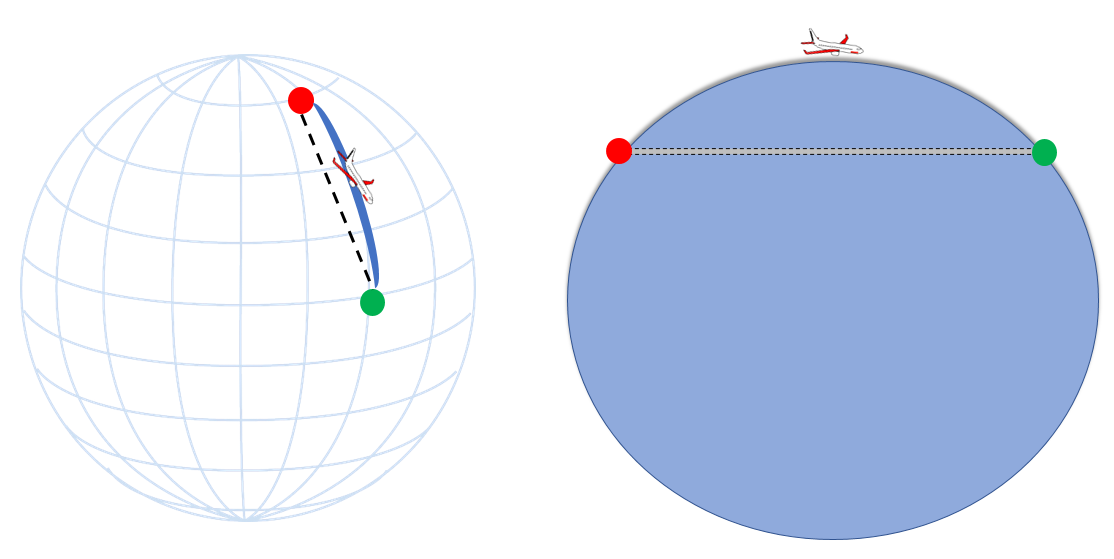
Earth is a sphere (unless you are one of these guys) and even when you travel in a seemingly straight line, you are bound to follow earth’s curvature. And this is the reason we can not use the Cartesian distance for calculating the distance between the two points.
Then, how can you find distance between two geographic locations if you just know their latitudes and longitudes?
We use something called “Spherical Law of Cosines“ that gives distance between two points on a sphere.

This formula may look complicated but it’s easy to implement. Download the Excel file to see this formula in action.
Assumptions
Circuitory Factor
The spherical distance formula gives distance “as the crow flies”. But roads are never a straight line – they zig-zag around natural obstructions and take detours to towns and cities on the way. To account for these curves of the road, we multiply our straight-line distance by a Circuitory factor. Typically, this factor is assumed to be 1.18
That is, the actual road distance is 18% more than the straight-line distance given by spherical formula.
This Circuitory Factor (also known as Detour Index) varies from geography to geography – coastlines and mountainous regions will have higher factor than plains.
For more details you can refer to other relevant articles here and here.
Earth isn’t a perfect sphere
Earth is an oblate, and that is the reason why neither the top of the Mount Everest is the farthest point from the centre of the Earth nor the bottom of Mariana Trench is the closest.
But this oblateness means that our spherical formula isn't perfect especially over large distances.
Natural obstacles
While using the distance formula, be wary of any natural obstacles that will have an impact on the route. This is especially true for mountainous regions, archipelagos, or any other regions where the movement between the two locations takes indirect routes.
Was this post useful? If you have any additional questions, feel free to drop a comment below.
 Hola! Detectives. With the previous series of articles on
Hola! Detectives. With the previous series of articles on 

 Have I landed on a wrong blog by mistake? Why the heck we are talking about finance on a supply chain blog?
Have I landed on a wrong blog by mistake? Why the heck we are talking about finance on a supply chain blog?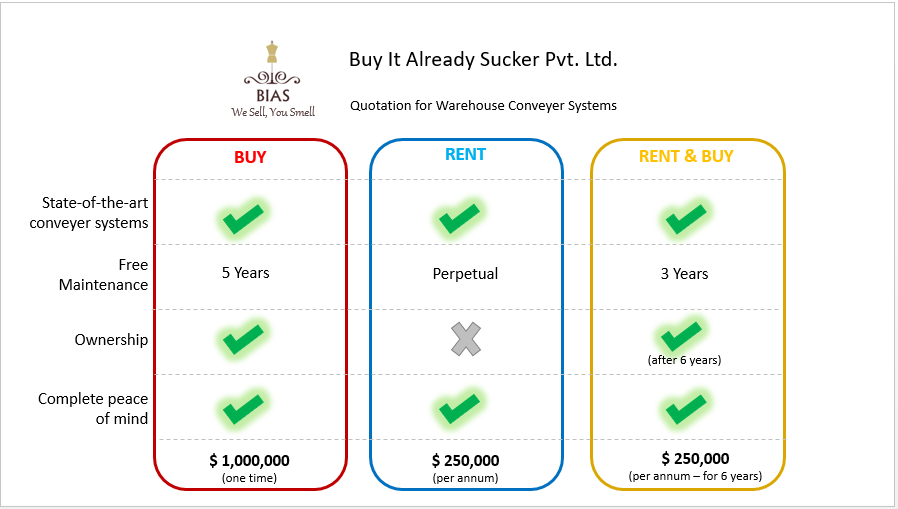


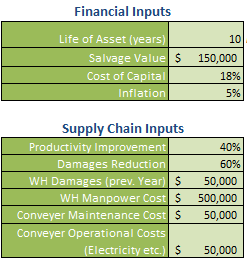
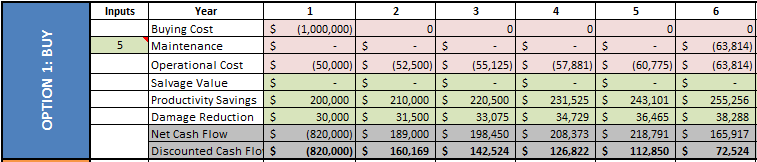
 Let us start with a very simple example– we have two sets of standard six-sided die with us. We would like to know what are the chances of getting a total of “7” when we roll them. You can get seven by several possible combinations, say, by getting “5” on one die and “2” on other, “6” on one die and “1” on other. In fact, there are more ways to get “7” than, say, getting “2” which can only be achieved in one way - by rolling “1” on both the dice.
Let us start with a very simple example– we have two sets of standard six-sided die with us. We would like to know what are the chances of getting a total of “7” when we roll them. You can get seven by several possible combinations, say, by getting “5” on one die and “2” on other, “6” on one die and “1” on other. In fact, there are more ways to get “7” than, say, getting “2” which can only be achieved in one way - by rolling “1” on both the dice. 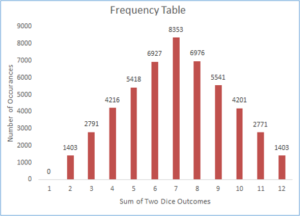
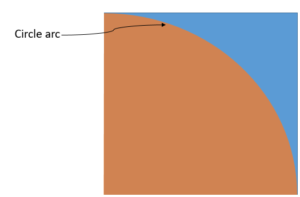
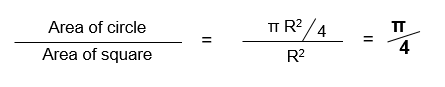


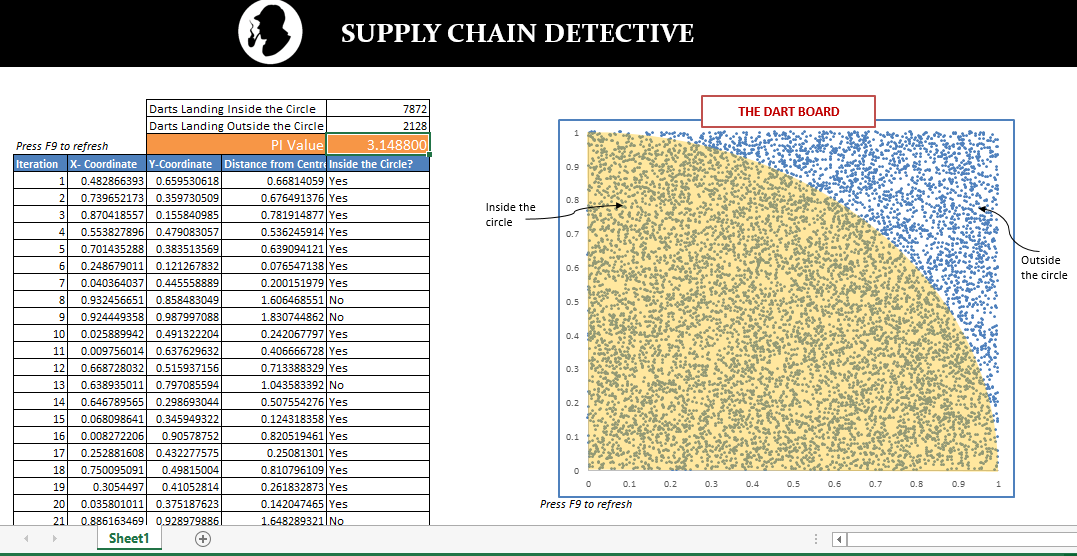
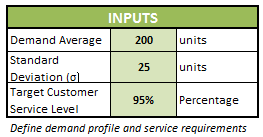
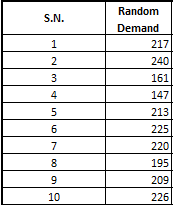
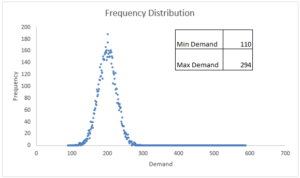
 Whenever you pick-up that joystick for shooting aliens, running through cross-dimensional portals or hopping
Whenever you pick-up that joystick for shooting aliens, running through cross-dimensional portals or hopping 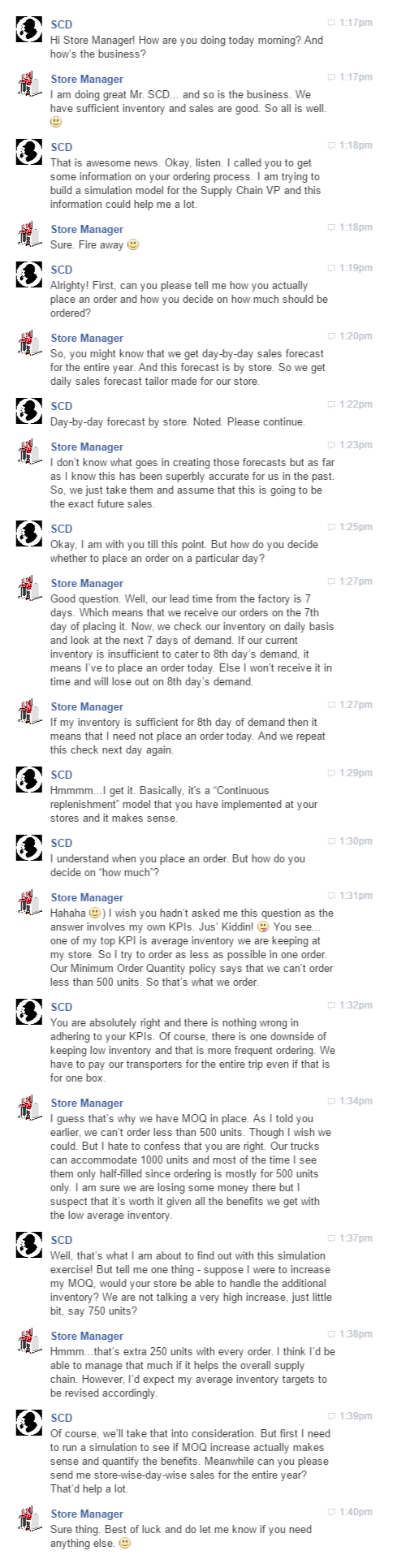
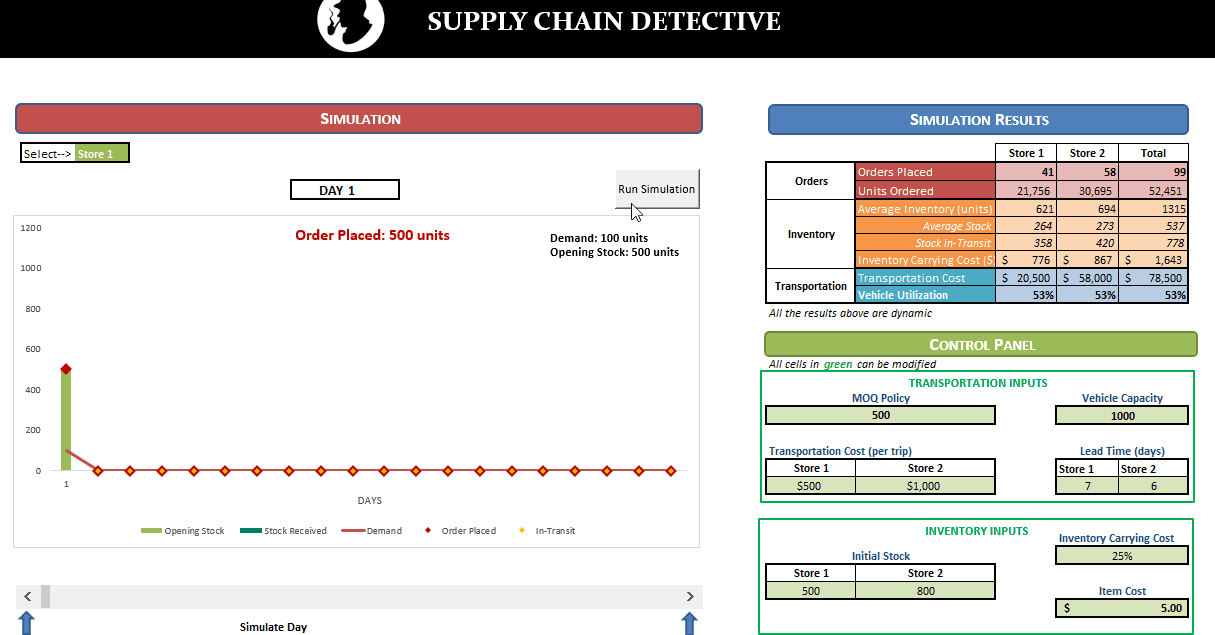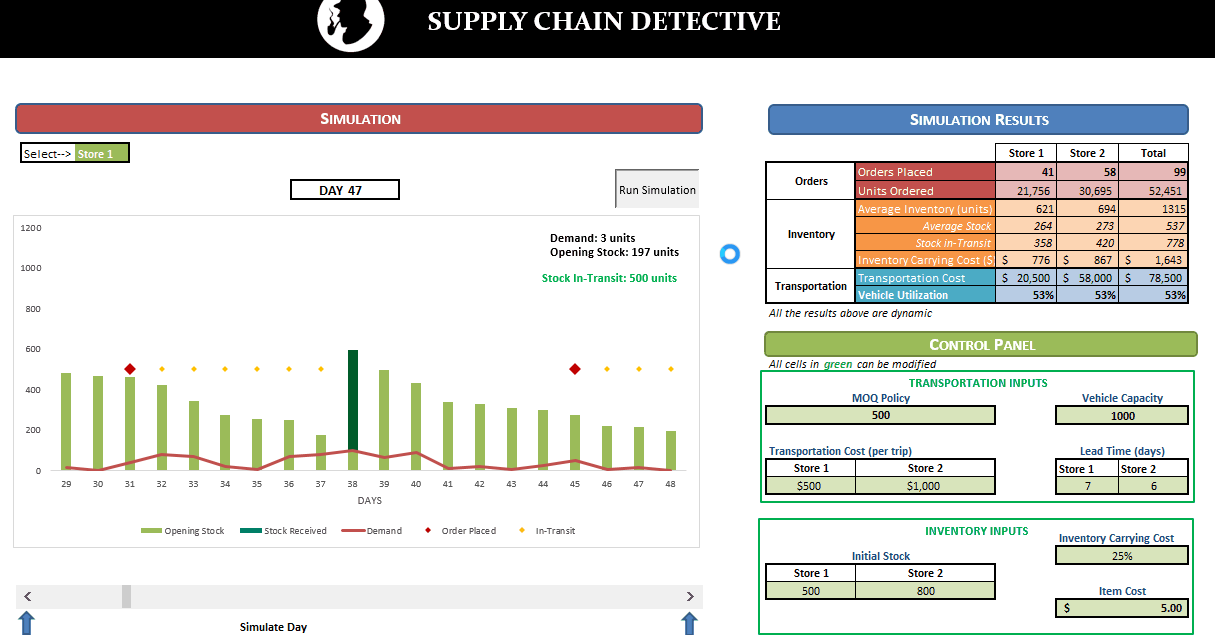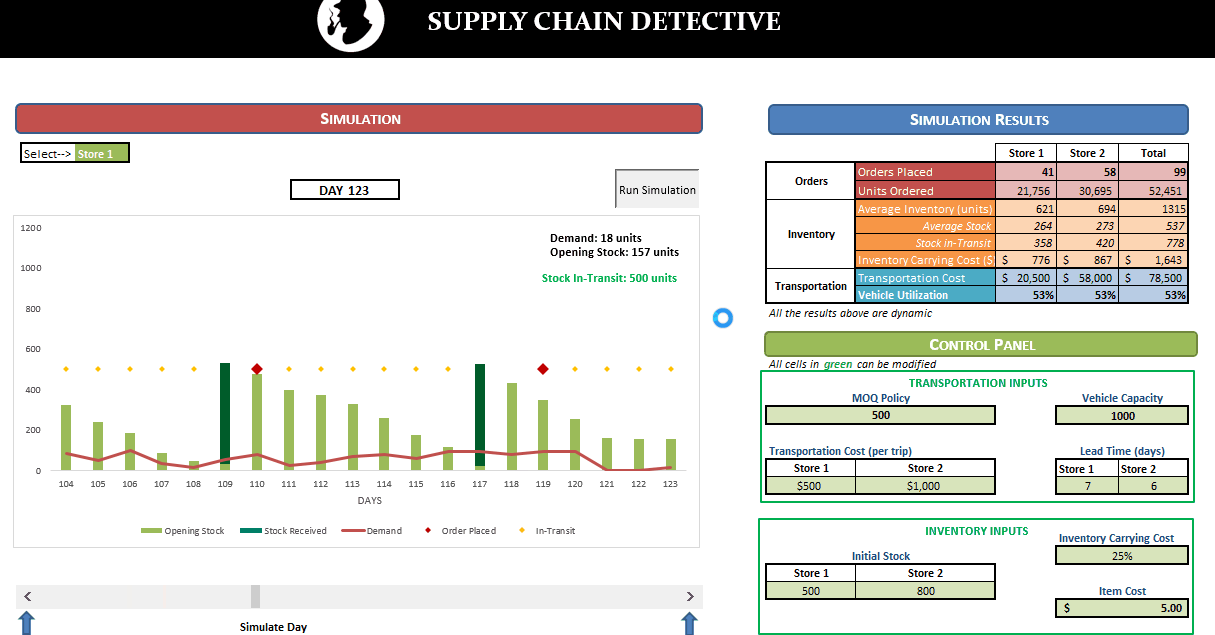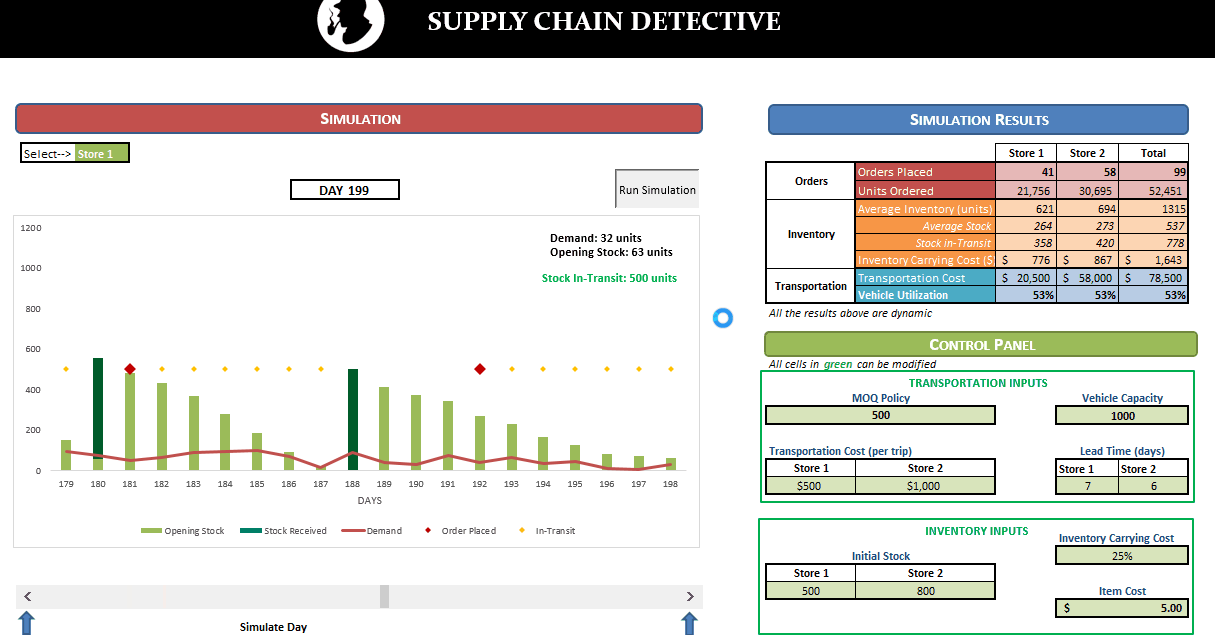
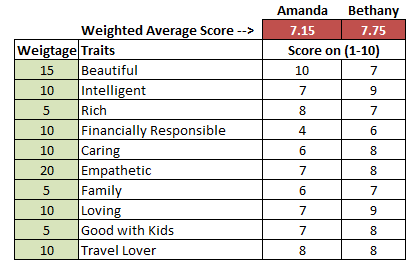

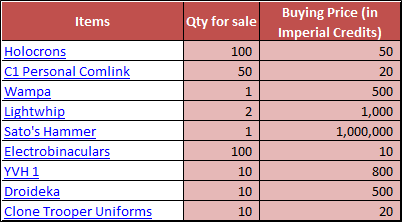
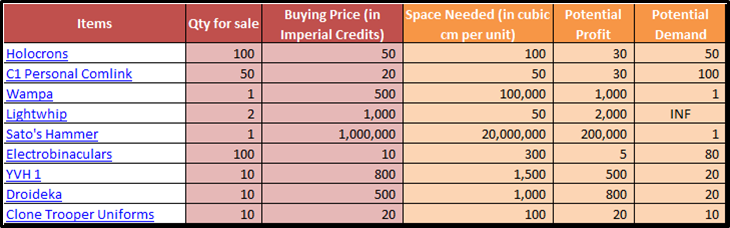
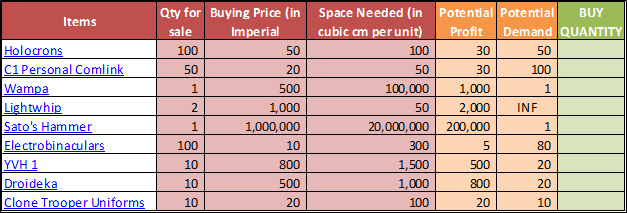

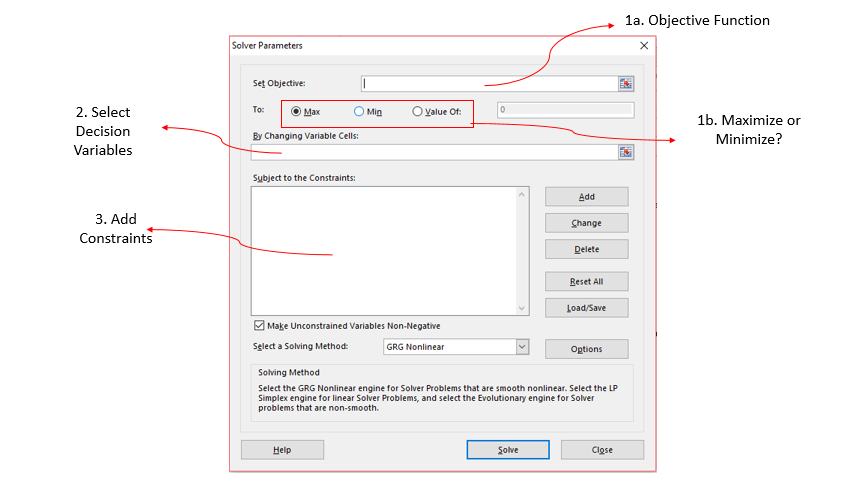
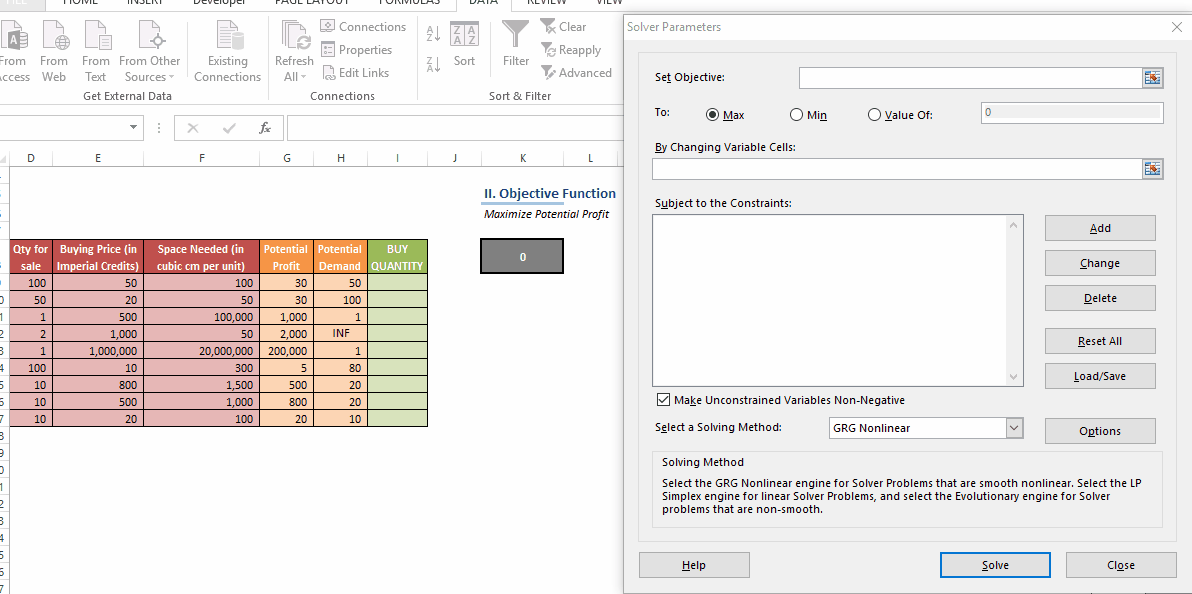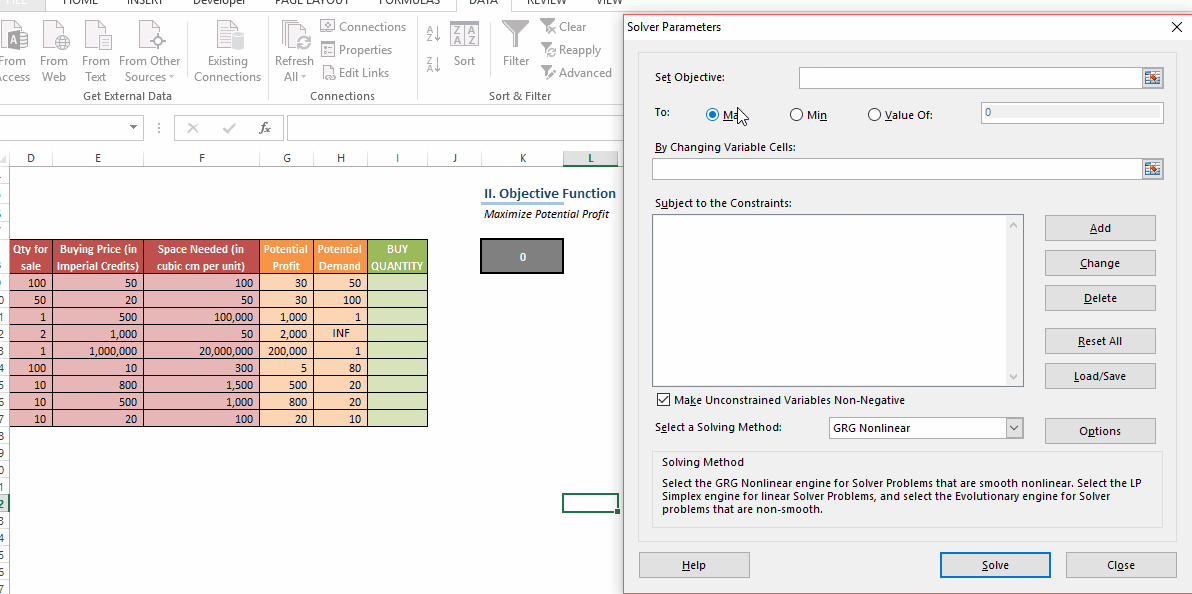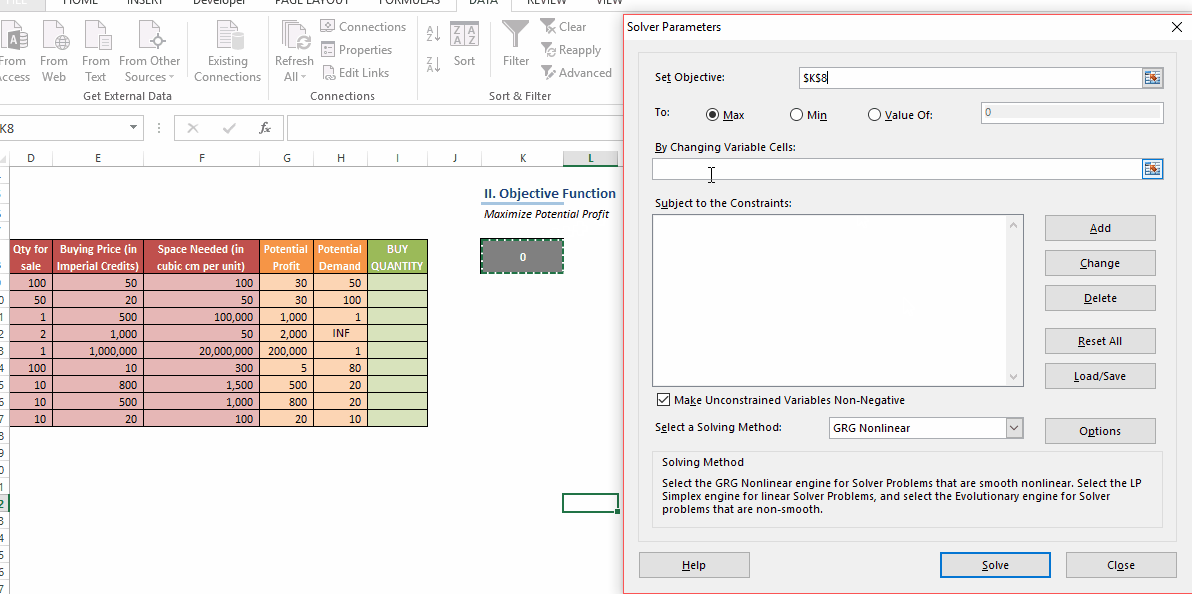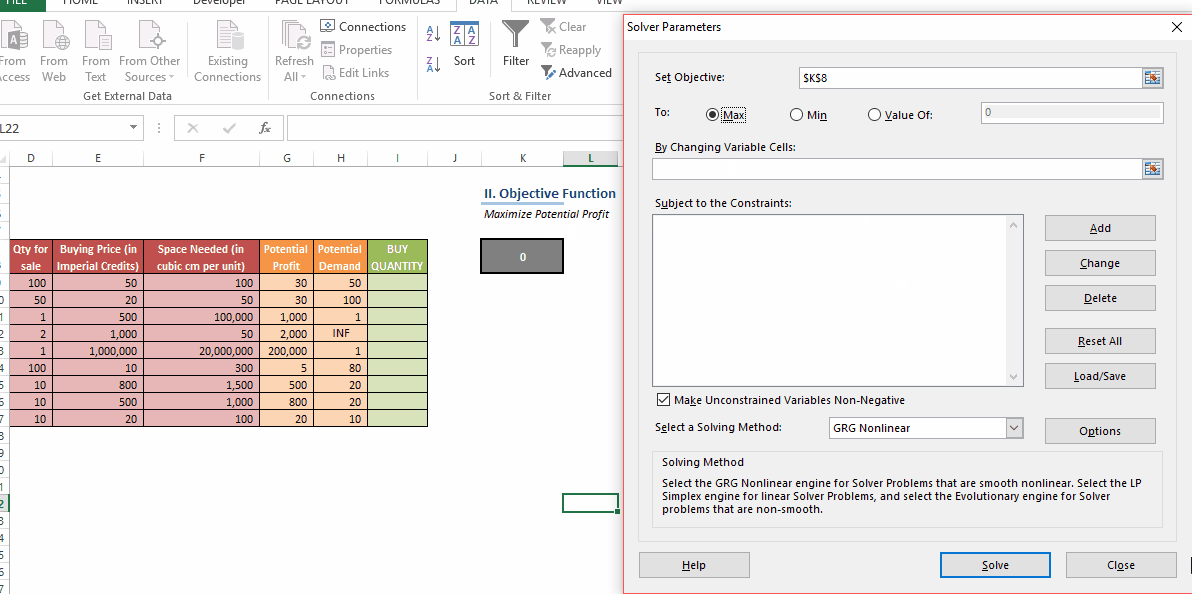
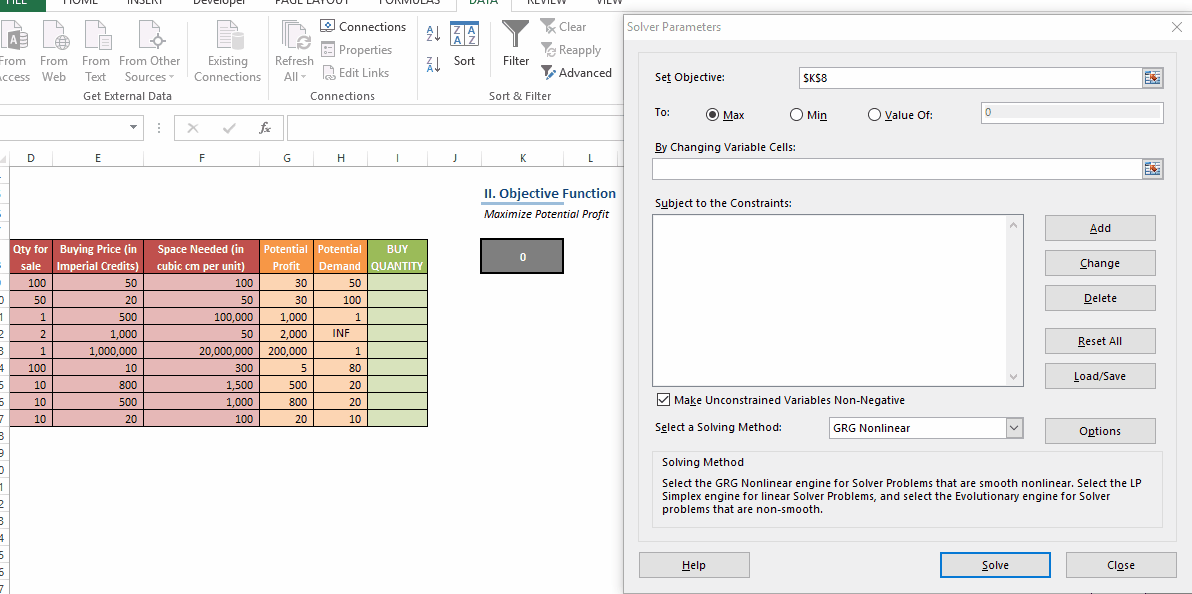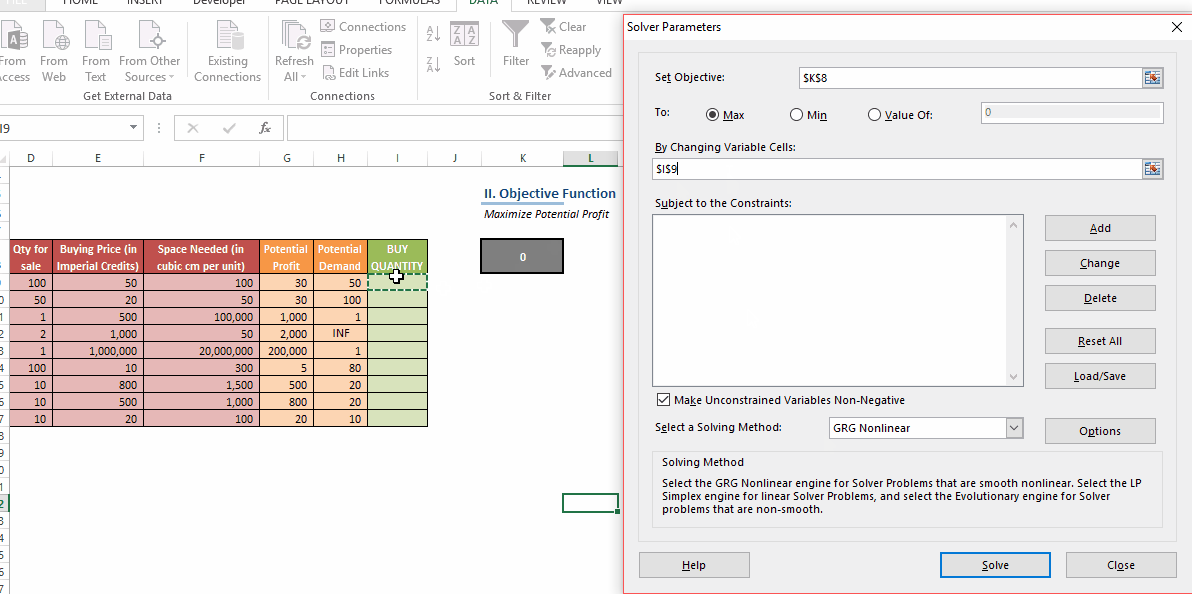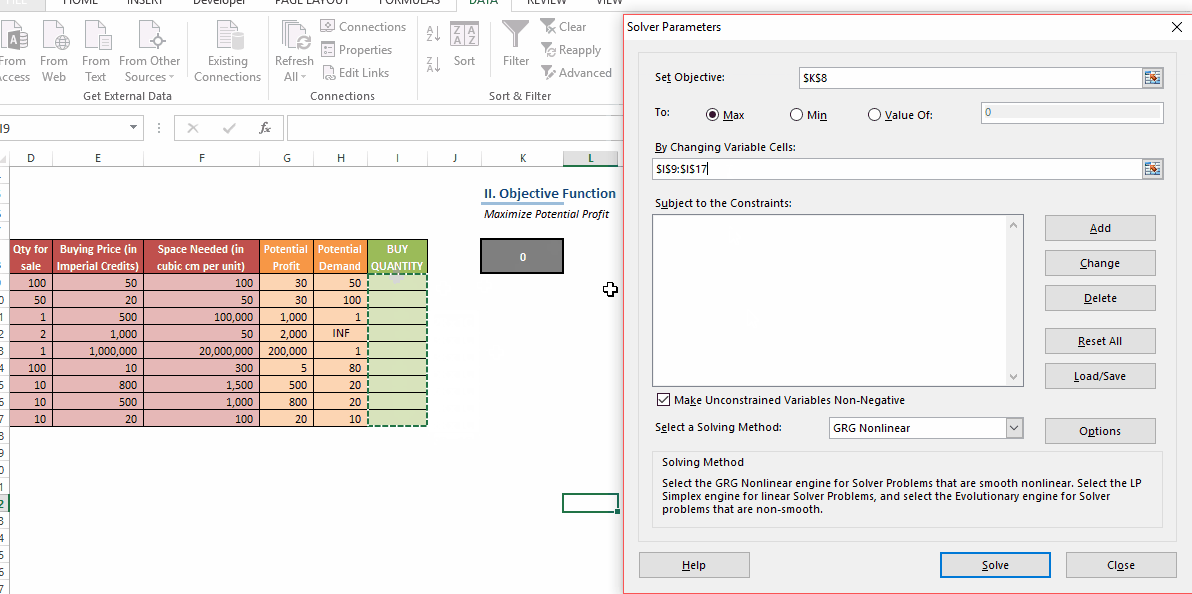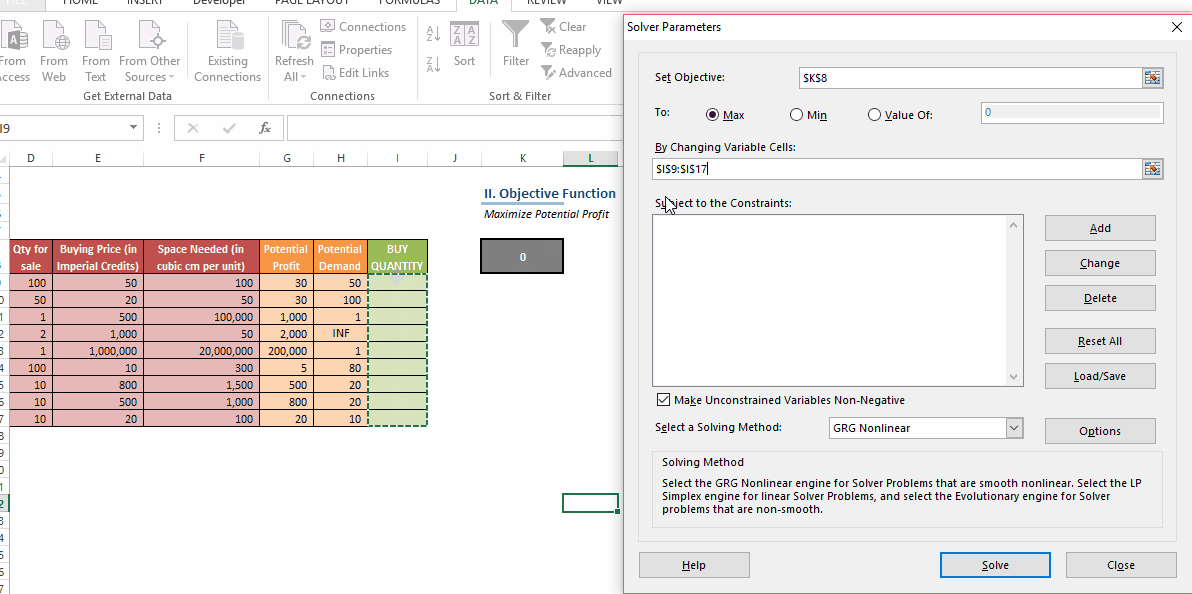
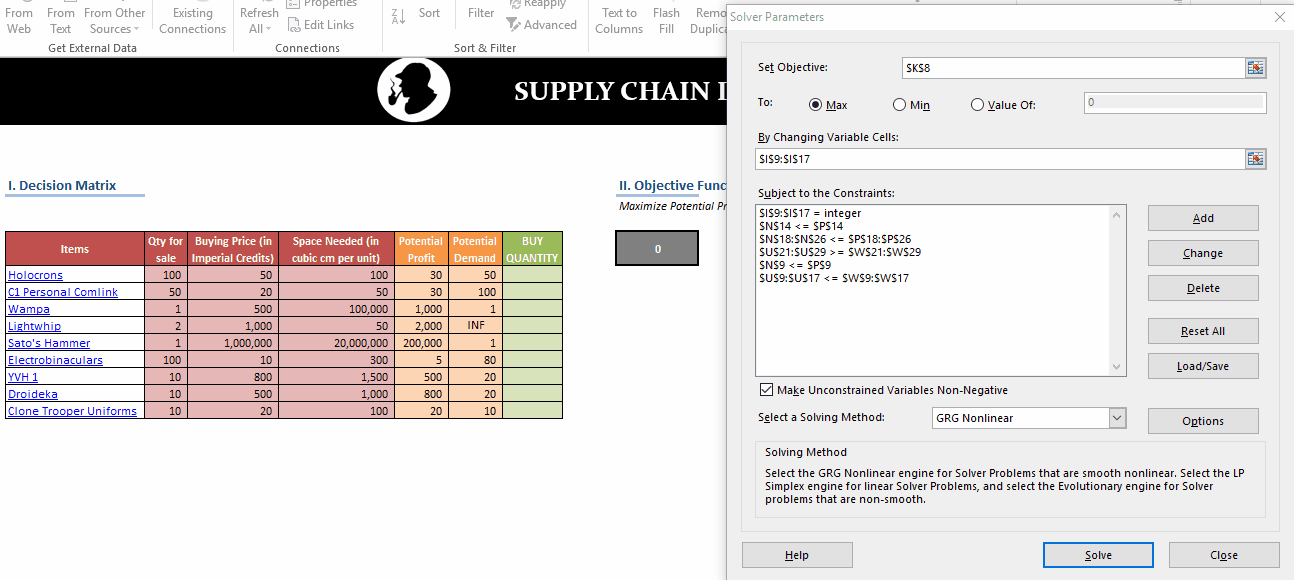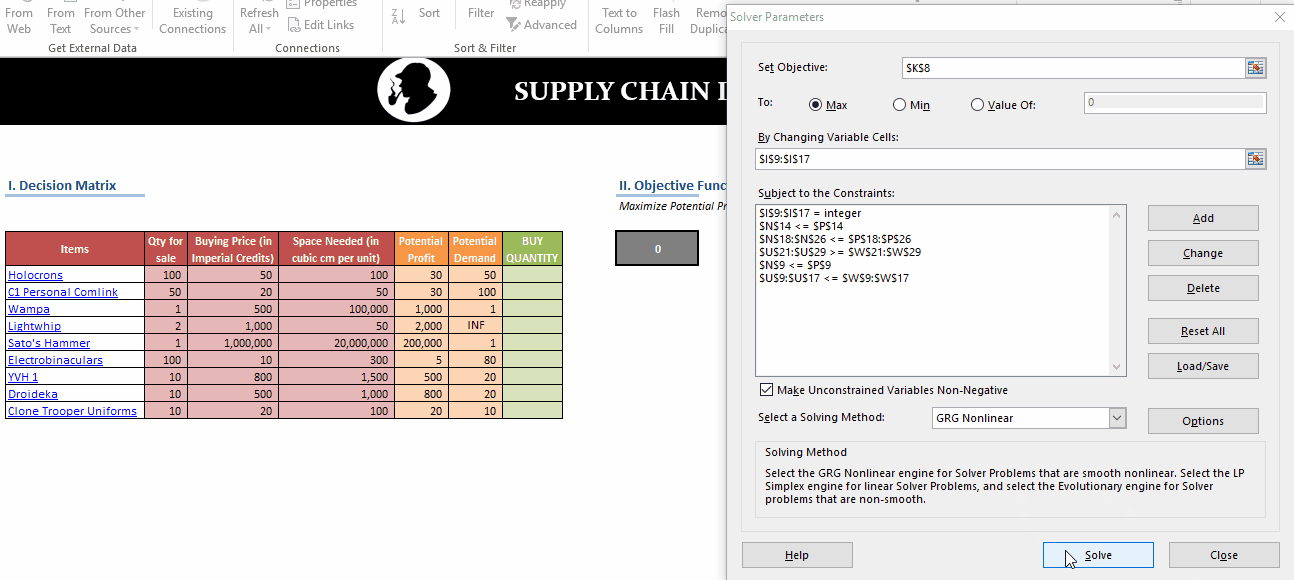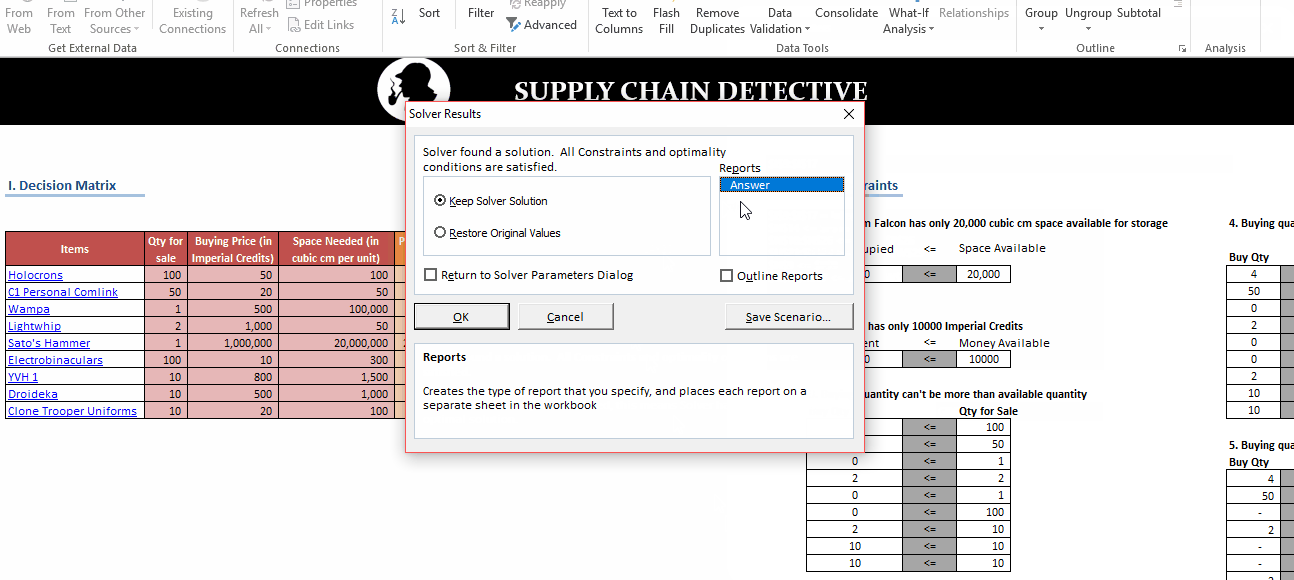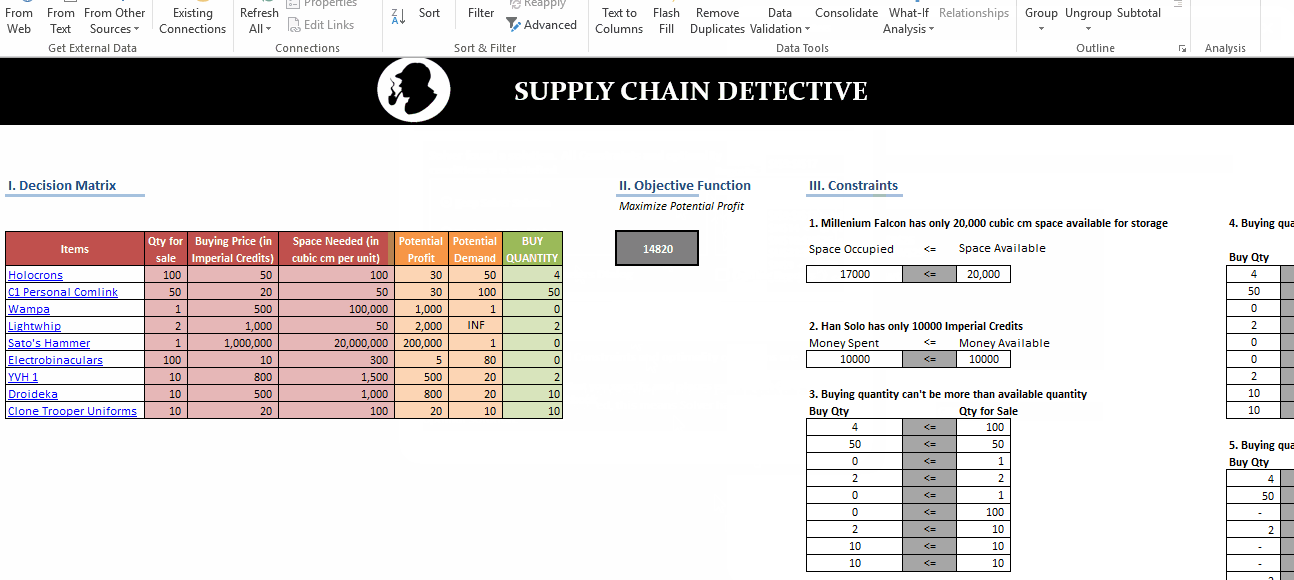
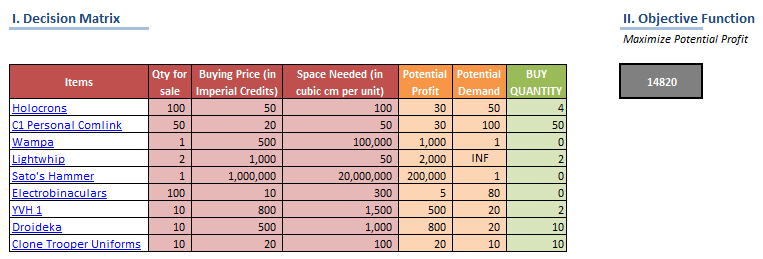
 In this post, we’ll be looking at some tips and tricks that will improve your model structure and polish rough edges in your model. Individually, these seem like minor tidbits but sooner you inculcate these “hacks” as part of your day-to-day work, sooner you’ll realize that your thought process has become much more structured and your output significantly better than your colleagues. With some practice, before you know it, you will be that rare person in your organization who can translate seemingly insurmountable data into brilliant insights.
In this post, we’ll be looking at some tips and tricks that will improve your model structure and polish rough edges in your model. Individually, these seem like minor tidbits but sooner you inculcate these “hacks” as part of your day-to-day work, sooner you’ll realize that your thought process has become much more structured and your output significantly better than your colleagues. With some practice, before you know it, you will be that rare person in your organization who can translate seemingly insurmountable data into brilliant insights.
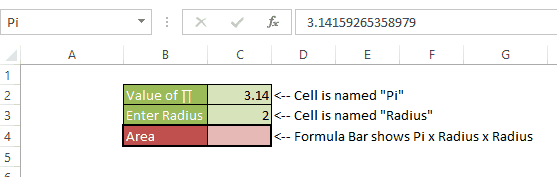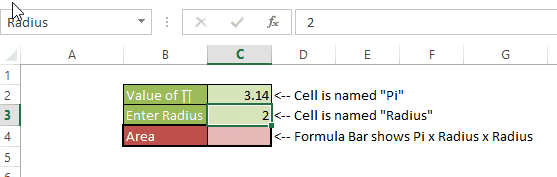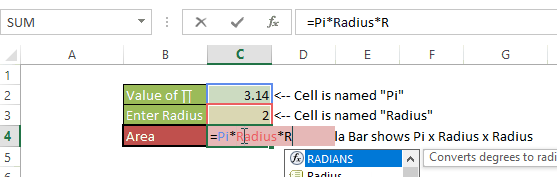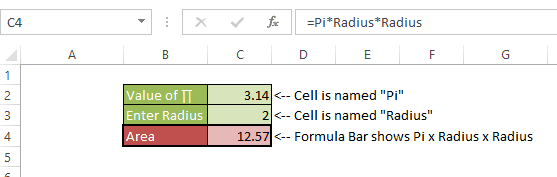

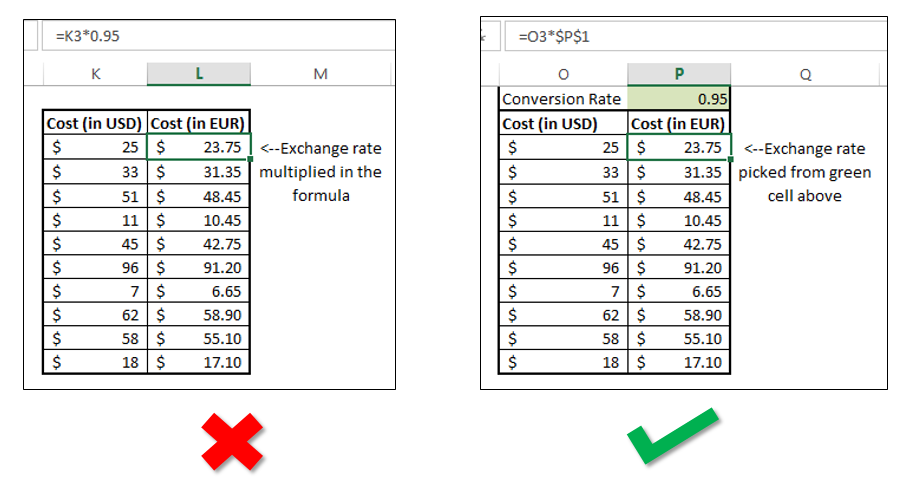
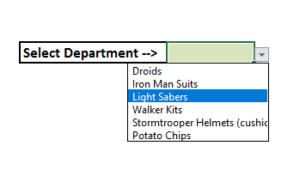
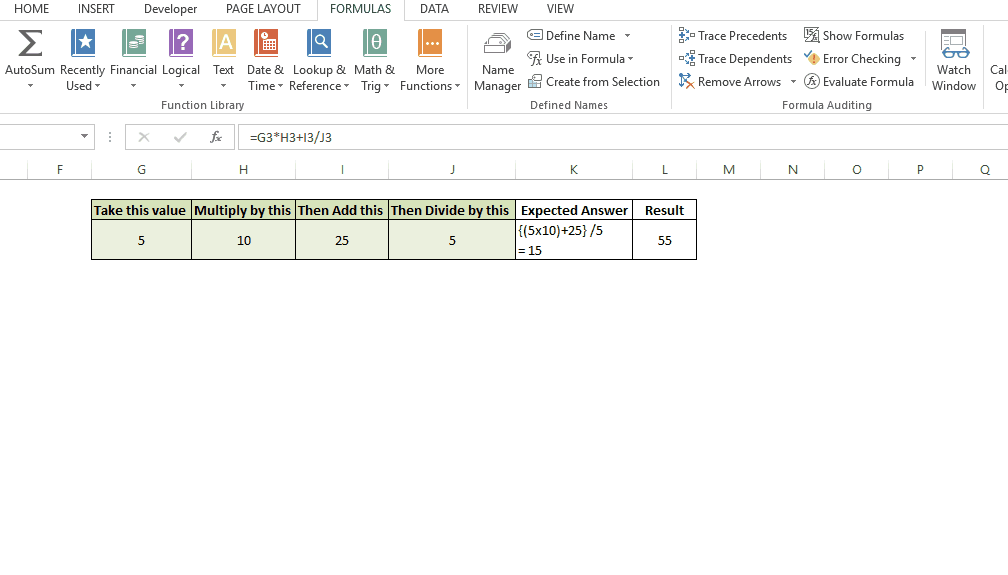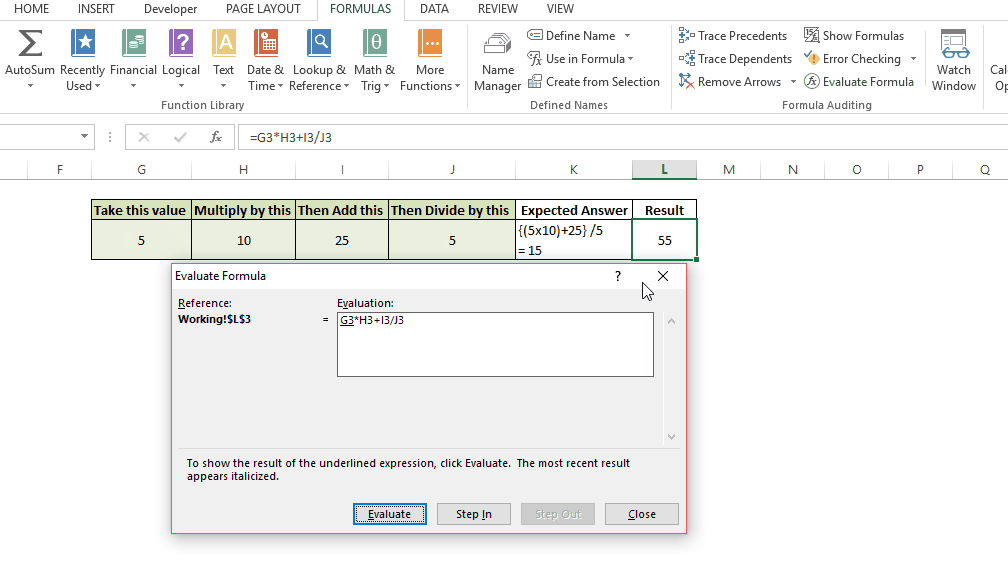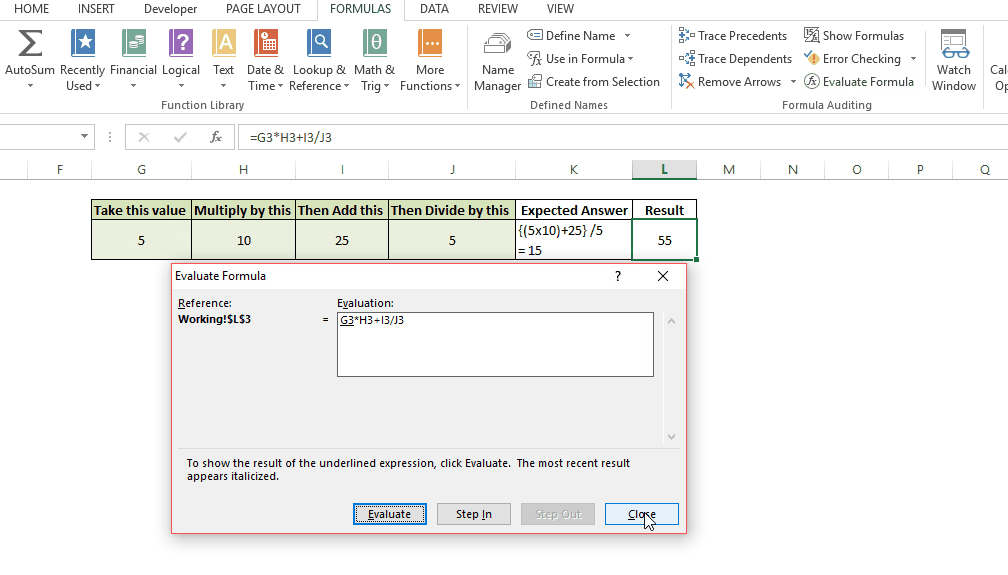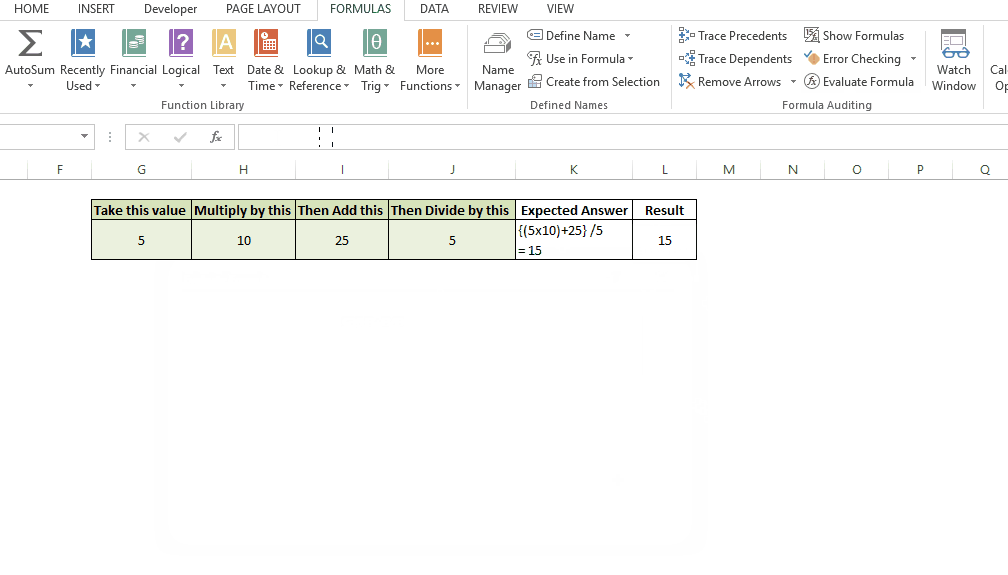
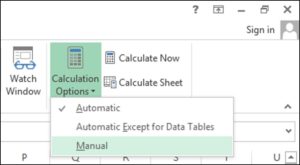


 You can be the best thing that has happened to the mankind since sliced bread, but if you don’t have proper skills to make sense of the data you might as well be a potato sitting on your boss’s chair.
You can be the best thing that has happened to the mankind since sliced bread, but if you don’t have proper skills to make sense of the data you might as well be a potato sitting on your boss’s chair.

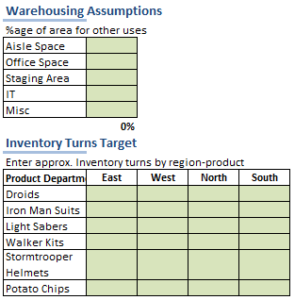
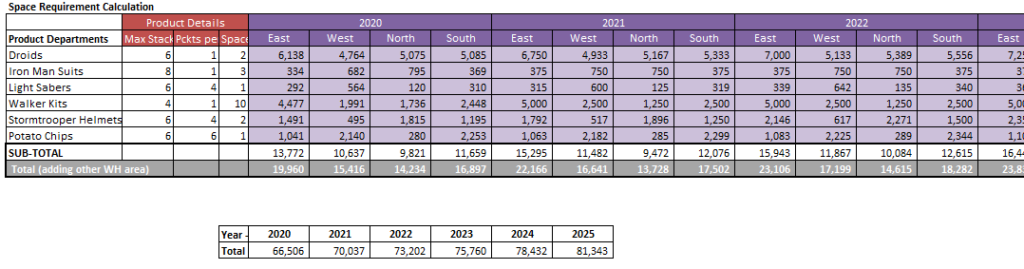

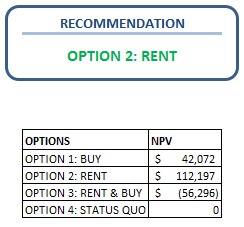
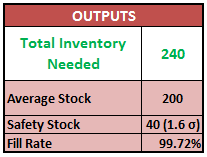
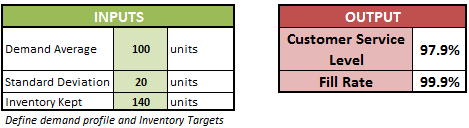
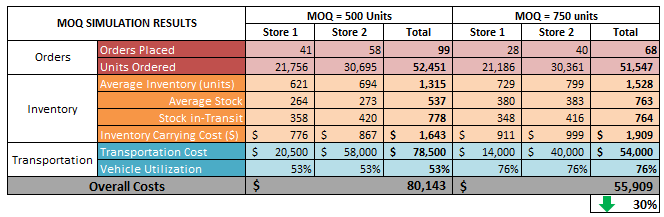
 This is one of the most contentious questions that is often raised in review meetings especially during months of high inventory. We’ve all been there - where all the inventory indicators are in red, warehouses are overflowing with stuff, several leaning Towers of Pisa in the DCs are a common sight and trucks are waiting for hours to unload their stuff. The supply chain VP’s phone is ringing non-stop and when it seems that nothing can go worse, you suddenly realize that you have an S&OP meeting to attend to.
This is one of the most contentious questions that is often raised in review meetings especially during months of high inventory. We’ve all been there - where all the inventory indicators are in red, warehouses are overflowing with stuff, several leaning Towers of Pisa in the DCs are a common sight and trucks are waiting for hours to unload their stuff. The supply chain VP’s phone is ringing non-stop and when it seems that nothing can go worse, you suddenly realize that you have an S&OP meeting to attend to. rs for your company. But before you knock on the corner office of your CEO or Supply Chain VP, be prepared to answer some questions that will be thrown your way.
rs for your company. But before you knock on the corner office of your CEO or Supply Chain VP, be prepared to answer some questions that will be thrown your way.