Good to see that you have made to part-II of this article. If you have not done so yet, I strongly recommend you to check-out the first part where we derived this deceptively simple EOQ formula.
Good to see that you have made to part-II of this article. If you have not done so yet, I strongly recommend you to check-out the first part where we derived this deceptively simple EOQ formula.
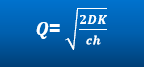
Where,
Q is Economic Order Quantity
D is Annual demand (in units)
K is Ordering Cost (in $) per order
c is Cost of the product (in $ per unit) and,
h is the inventory carrying cost (as %age of product cost, incurred annually)
In this post we’ll see why EOQ formula should be rarely used in its basic form. And even if you were to use it, you must at least be aware of the caveats and assumptions that have gone into it.
We’ll do that in two parts. First let us challenge some assumptions that we made earlier and then we’ll put in some real world complications that require us to tweak the formula or add in some layers of analysis before we start using the order quantity recommendations.
Assumption #1: Inventory Depletion is uniform
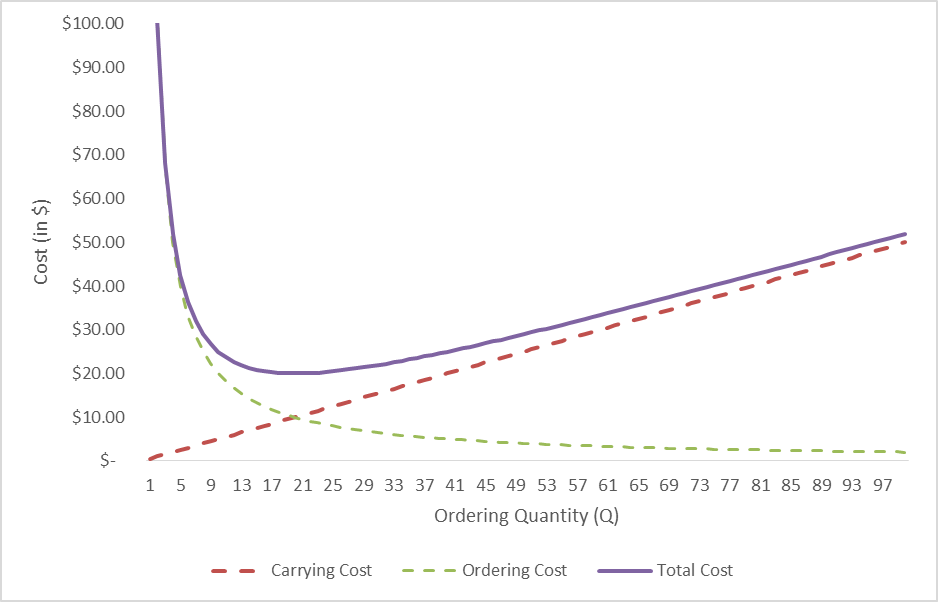
One of the major assumption while deriving the formula was uniform inventory consumption. And that is how we arrived at Q/2 as average inventory. However, this is seldom true. Rate of consumption changes from season to season, week to week and even day to day.
Solution: An ideal solution is to come up with a consumption curve (Inventory vs Time graph) and use it to calculate average inventory over time. However, this may involve doing an integral of a complex curve. If you want to be super-precise then that’d the way to go but there are more practical and easier approximations to this problem that will give you “good” solutions with a lot less effort.
Approximation: Rather than one continuous curve, we can break our time period into two or more sub-periods each having a simpler consumption pattern. For example, a vast majority of FMCG organizations make most of their sales during the last week of the month. This could be a typical case of student syndrome where sales team is pushing to meet their monthly targets. [This takes a significant toll on supply chain infrastructure and many organizations struggle to manage these last week peaks. We will dedicate a separate post to this topic.]
So, let us say that 50% of the monthly demand is consumed in first three weeks while remaining 50% is consumed in last week itself. In other words, consumption rate during last week is thrice that of first three weeks. Over long-term1, the average inventory can be calculated to be 5Q/8. We leave it to the readers to derive this number. You may notice that this average inventory is higher than (Q/2) that we calculated earlier where the inventory depletion was uniform throughout. This makes sense as earlier we had consumed 75% of the monthly demand in 3 weeks whereas we have only consumed 50% in the current scenario, leaving us with slightly higher inventory.
If we put 5Q/8 as average inventory in Total cost equation:
![]()
We can derive modified EOQ as:
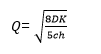
Similarly, now you can derive your own EOQ formula given any consumption rate or consumption pattern.
Assumption #2: Cost of the material is constant regardless of quantity
Remember when we wrote the total cost equation as
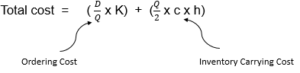
We deliberately didn’t consider one element of cost in the above equation which was buying cost. We ignored it because it wasn’t relevant as we were spending the same amount annually despite of ordering quantity.
However, this assumption doesn’t hold true especially when buying quantities are large. Suppliers often provide bulk discount options as they save on producing at a scale. In fact a typical supplier quote looks like this:
QTY |
1-20 |
21-50 |
51-100 |
101-150 |
151+ |
Price (per) |
$ 5 |
$ 4.75 |
$ 4.5 |
$ 4.25 |
$ 4 |
As the quantity increases our buying cost decreases significantly. In fact supplier is willing to offer 20% discount if we buy more than 150 units of the product. But is it worth it?
Now, let us rewrite the total cost equation, this time around we’ll have to include the buying cost as it has become relevant.
![]()
The product price c* is now a function of Q –
c* = $ 5 per unit (for Q between 1-20)
c* = $ 4.5 per unit (for Q between 21 -50)
...and so on.
Graphical Solution
Let us recreate the chart that we made earlier. This time around, we have an additional line for buying cost.
Download the workbook HERE.
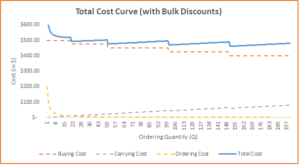
As you can see in the graph above, buying cost is a step-curve. Those “steps” represent the bulk-discounts that supplier has offered. We also see these “steps” in total cost curve (the thick blue line) since it includes the buying cost. You’ll notice that now it is not so easy visually to find the minimum cost point on the total cost curve.
I checked the table that was used to create the graph in the workbook, and it turns out that minimum total cost is $ 461.7 while buying 151 units. Note that this is different from our non-discounted EOQ number where we got the answer as 20 units.
How will you sell this to the CEO? You can’t show derived EOQs and complex graphs, right? Well, you can simply state the following – “Usually, we should only buy 20 units at a time which is roughly one month of supply, however this time around the supplier is giving 20% discount on bulk orders. Sure, this increases our inventory costs a bit but it’ll be more than compensated by the discount.”
Interestingly, the next lowest cost $ 470 occurs at 101 units. So, if your CEO still frowns at you for asking to buy huge inventories, you can always fall back on the second best solution, where incurring 9 dollars extra reduces your inventory from 150 to 100.
[The second best or even third best solution may be more acceptable in some cases. True – that absolute minimum occurs at 151 units but just paying additional 9 dollars we can mitigate some of the unaccounted risks that come along with the additional inventory. This is a typical problem with all kinds of optimization algorithms. They try to reduce the objective function to the absolute minimum, a phenomenon that we describe as chasing the pennies. This is sometimes not desired. And this is where multi-objective optimization comes handy. However, that is another discussion for some other day.]
Analytical Solution
Above, we arrived at the solution by looking at the graph and corresponding data but that’s not feasible especially when large quantities are involved or we don’t have access to spreadsheet software.
While there is no straightforward formula for EOQ with bulk discount because buying cost is a step-function and hence non-differentiable, we still have a step-by-step procedure that can help us arrive at the best quantity.
Step 1: Find normal EOQ for ALL buying costs
In our example, there are five different costs. While we are not showing the detailed calculation their corresponding EOQ values are shown below. Subscript represents the cost(in $ per unit):
EOQ5 = 20 units
EOQ4.75 = 20.5 units
EOQ4.5 = 21.1 units
EOQ4.25 = 21.7 units
EOQ4 = 22.3 units
[Bonus Question: Keeping all the other factors constant, why does EOQ increases as the cost per unit decreases?]
Step 2: Eliminate “Invalid” solutions
Some of the EOQ quantities doesn’t belong to the buying cost. Eliminate them.
EOQ5 = 20 units
EOQ4.75 = 20.5 units X
EOQ4.5 = 21.1 units X
EOQ4.25 = 21.7 units X
EOQ4 = 22.3 units X
Note: You may be left with none or more than one solutions.
Step 3: Calculate and compare total costs for all the valid EOQ solutions and buying qty break-points
Qty Type |
Qty (units) |
Total Cost ($) |
EOQ5 |
20 |
520 |
Bulk Qty 1 |
1 |
701.5 |
Bulk Qty 2 |
21 |
494.5 |
Bulk Qty 3 |
51 |
476.9 |
Bulk Qty 4 |
101 |
469.9 |
Bulk Qty 5 |
151 |
461.7 |
Total minimum cost is at Qty 151 which is our answer.
Assumption#3: Inventory Carrying Costs are constant
As briefly touched upon in previous part of this article, inventory carrying cost consists of several components – cost of capital (typically the borrowing rate of your organization), cost of storage (Warehousing costs and salaries) and cost of servicing the inventory (insurance, damages, obsolescence). Though it is highly organization dependent, finding the exact value might be a tricky task. It is usually taken between 17% and 25% depending the nature of the inventory and opportunity cost of capital to the organization.
However, some of these variables are not constant and vary with the quantity of inventory kept in the organization. Couple of examples are below:
Insurance cost: Per unit insurance cost decreases as average inventory increases.
Risk of damages/obsolescence: Risk of damages and obsolescence increases as average inventory increases.
Solution:
The solution requires some understanding of basic differentiation. If you don’t get it in the first attempt, don’t worry about it too much.
Let us say that by some measure of analytics, one has arrived on a inventory carrying cost equation
Inventory Carrying Cost (h)= r + f(Q)
h = 20% + 2%* [(Q/(D/12)]
Don’t get scared by the above equation. It simply states that inventory carrying cost is 20% plus 2% for addition of every month to order quantity. This 2% is attributed to the increasing risk because of incremental inventory. Hence for one month’s inventory, carrying cost = 22%, for two months its 24% and so on.
Putting this in the basic equation
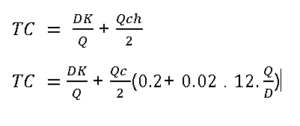
Differentiating both sides by dQ
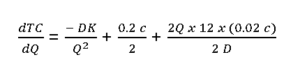
For min TC,
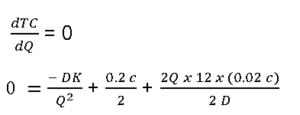
Simplifying the equation we get,
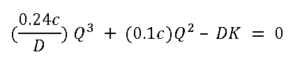
Replacing the variable values, D = 100 units, c = $ 5, K = $2
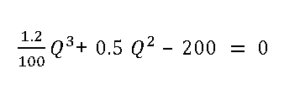
This is a cubic equation with three solutions for order quantity Q.
Q= 16.87, -29.2 ±11.44i
We can reject the complex solutions. Hence, the EOQ for dynamic carrying cost is ~ 17 units.
Note that this is slightly lower than our original solution of 20 units that considered fixed carrying cost of 20%. This seems logical as slight increase in carrying cost is reflected in decreased EOQ.
Conclusion
If you have reached this far, then CONGRATULATIONS! You’ve mastered the science behind ordering quantities and their trade-offs, you are now ready to take on any challenge that anyone in your organization can throw at you. Well, let me scratch that. You are almost ready.
There are some teeny-weeny complications that are often put to question your EOQ numbers. While some of those do not impact our EOQ too much, it is important to be aware of them to pave way for smooth implementation of your ideas. Part 3 of this article is dedicated to those complications and work-arounds.
[Boy, I never realized that this simple EOQ formula would take me 3 parts to finish. Well, grab some coffee and click on part 3]
Footnotes:
1 Order quantity may or may not be equal to one month’s demand. Hence, every month’s inventory profile will look different. E.g. if order quantity = 5 weeks, 1st month will see an ending inventory of 1 week, 2nd month will see ending inventory of 2 weeks and so on. Hence, we look at long term average of the inventory.
 If you asked any CEO, Sales Executive or Marketing head what is the customer service level they desire in the organization they’d invariably say 100%. And hearing that answer the Supply Chain VP will invariably shake their heads and flee the room before you could ask them the same question.
If you asked any CEO, Sales Executive or Marketing head what is the customer service level they desire in the organization they’d invariably say 100%. And hearing that answer the Supply Chain VP will invariably shake their heads and flee the room before you could ask them the same question. n zombies (SCZs), who are now vying for the blood of the crackpot who wrote such a blasphemy as the title of this post, take a deep breath, cool down a bit and think back at the time when you last implemented the EOQ formula in its basic form. That is – NEVER.
n zombies (SCZs), who are now vying for the blood of the crackpot who wrote such a blasphemy as the title of this post, take a deep breath, cool down a bit and think back at the time when you last implemented the EOQ formula in its basic form. That is – NEVER.